Equivalent Circuit Elements and Parameters

a). Capacitor (C). Capacitor contributes to the imaginary part of the impedance:
                                   Z(ω) = (j*ω*C)^-1
where j is imaginary unit, ω is angular frequency, the parameter C is capacitance (F)


b). Resistor (R). Resistor with resistance R (Ohm) contributes to the real part of impedance:
                                              Z(ω) = R

c). Warburg (W). Warburg element represents the impedance of semi-infinite diffusion to/from flat electrode. This element contributes equally to the real (ReZ) and imaginary (ImZ) parts of impedance:
                                 ReZ (ω)   = A_W /ω^0.5
                                 ImZ (ω)    = - A_W /ω^0.5
where A_W is the Warburg coefficient (Ohm s^-0.5):



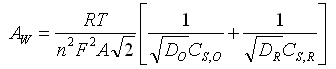
R - universal gas constant, T - absolute temperature, n - number of electrons, A - electrode surface area, D - diffusion coefficient of the electroactive species, C_S,O , C_S,R - surface concentrations of oxidized and reduced form.

d). Constant Phase Element (CPE). CPE is an element used often in modelling the ac response of non-homogeneous systems. CPE has two parameters: Q and n and impedance of this element is given by the formula: 
                                              Z(ω) = Q^-1(j*ω)^-n
Q becomes equal to capacitance, when n = 1. Similarly to capacitor, CPE keeps the phase constant at variable frequency but the phase shift differs from 90^°. CPE is especially helpful  for representing slightly distorted capacitances.

e). Inductor (L). Impedance of the inductor is given by the formula:
                                                      Z(ω) = j*ω*L
where the parameter L is the inductance.

f). Warburg Short (W_s). Impedance of finite-length diffusion with transmissive boundary. This element has two parameters: W_Sr and W_Sc. Impedance of W_S element is given by the formula:


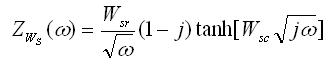
where W_Sr is equal to Warburg coefficient, W_Sc = d/D^0.5, d - Nernst diffusion layer thickness.

g). Warburg Open (W_o). Impedance of finite-length diffusion with reflective boundary. This element has two parameters: W_Or and W_Oc. Impedance of W_O element is given by the formula:    


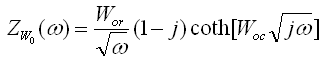
where W_Or is equal to Warburg coefficient, W_Oc = d/D^0.5.

h). Gerisher (G). Gerisher element has two parameters: Yg and Kg. Impedance of Gerisher element is given by the formula:
                                         Z(ω) = (Yg(Kg + j*ω)^0.5)^-1

i). User defined element (U-element). Though the ac response of a real object can be modelled adequately with a sufficient number of the basic predefined elements, the physical meaning of some elements in complex equivalent circuits may be not clear. U-element can be used in such cases to find the model hidden behind inexpressive elements. U-element allows testing various mathematical models of ac response. In this program the U-element with up to five parameters can be added to an equivalent circuit. Combining U-element with predefined elements can be useful when a part of ac response has a known origin (resistance of a solution, double layer capacitance, etc.) but the other part is of unknown origin. Modelling the remaining part by U-element can help understanding its origin. See instructions on how to use this element at U-element